DISTANCIA ENTRE PUNTOS
Para poder calcular la distancia entre
dos puntos primeramente debemos conocer las coordenadas de estos
puntos. Tomaremos dos puntos cualquieras para luego, a partir de estos generar un criterio para cualquiera sea
el par de
puntos a los que posteriormente calculemos la distancia.
puntos. Tomaremos dos puntos cualquieras para luego, a partir de estos generar un criterio para cualquiera sea
el par de
puntos a los que posteriormente calculemos la distancia.
Sean los puntos A=(x, y) y B= (w, z),
dos puntos que pertenecen al primer cuadrante del plano cartesiano.
Calcular la distancia entre ambos.
Calcular la distancia entre ambos.
Ejemplo:
Calcular la distancia entre los puntos
R= (5,6) y T= (2,2)
Para encontrar el punto medio del segmento utilizaremos los mismos puntos de la demostración
anterior. Entonces, calcularemos el punto medio del segmento AB. Para eso utilizaremos el
concepto de promedio, para calcular la distancia intermedia entre dos longitudes debemos calcular
el promedio de estas. Entonces ahora para calcular una distancia
Media entre dos puntos se deberá ocupar el mismo concepto. Se debe analizar por separado cada
eje coordenado y así se poder encontrar el punto medio, según los puntos encontrados para cada eje coordenado.
Ejemplo:
Calcular el punto
medio entre el punto (5,5) y el punto (9,3).
En el eje x el
promedio de las longitudes será
En tanto, el
promedio en el eje y será
Por lo tanto, el
punto medio es:
7.4
División de un segmento en una razón dada.
El resultado de la comparación de dos cantidades de la misma especie,
se llama razón o relación
de dichas cantidades. Las razones o relaciones pueden ser razones por cociente o geométricas.
La razón por cociente o geométrica es el resultado de
la comparación de dos cantidades
homogéneas con el objeto de saber cuántas veces la una contiene a la otra.
En geometría analítica
las razones deben considerarse con su signo o sentido porque se trata de
segmentos de recta dirigidos.
Consideramos como el proceso de “Dividir un segmento en una razón
dada” aquel el cual consiste
en determinar una posición (P) del elemento en cual se encuentra el suso dicho (Segmento) dado entre dos puntos (A)y (B), de tal manera que el segmento (AP) dividido entre el segmento (PB) da como resultado la razón.
R= AP/PB
Ahora, para obtener las coordenadas de un punto 'P', que divida a un
segmento
en una razón dada, se sigue las siguiente fórmulas: 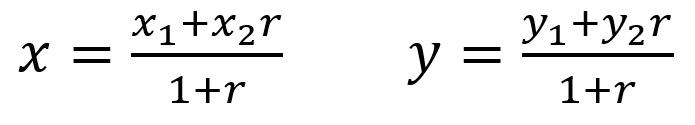
El valor de x2 se multiplica por la razón y se divide
entre la suma de 1 más la razón. Así, se
obtiene la abscisa del punto 'P'. La ordenada, se obtiene de manera análoga.
Ejemplo:
¿Qué puntos P y Q dividen al segmento de extremos A (-1, -3) y B (5, 6) en tres partes iguales?
BARICENTRO
El baricentro es el punto de corte de las tres medianas.
Las medianas de un triángulo son
las rectas que
unen el punto
medio de un lado del triángulo con el vértice opuesto.
El baricentro se expresa
con la letra G.
El baricentro divide
a cada mediana en dos
segmentos, el
segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
BG = 2GA
CORDENADAS DEL BARICENTRO
A(x1, y1), B(x2,
y2), C(x3, y3),
Las coordenadas del baricentro son:
Ejemplo
Dados los vértices de un
triángulo A (-3, -2), B (7, 1) y C (2, 7),
hallar las coordenadas del baricentro.
AREA DE TRIANGULO
Considere un
vértices del triángulo en el plano cartesiano (A x A, y A),
B (x B, y B), y C (x C,
y C).
El área de este triángulo es dada por:
Observe que el área
se obtiene multiplicando ½ por el módulo del determinante de las coordenadas
De los
vértices.
Ejemplo 1. Determine el área de un triángulo de vértices A (3, 3), B (6, 3) y C (3, 5).
Solución:
vamos a hacer el cálculo del determinante de las coordenadas de los vértices
del triángulo.
BIBLIOGRAFIAS
DISTANCIA
ENTRE DOS PUNTOS
-http://www.escolares.net/matematicas/distancia-entre-puntos-y-punto-medio/
PUNTO MEDIO
-http://www.escolares.net/matematicas/distancia-entre-puntos-y-punto-medio/
- https://sites.google.com/site/geometriaanaliticasmec3/division-de-un
BARICENTRO
- https://www.ditutor.com/geometria/baricentro.html
AREA DE UN TRIANGULO
- https://mundoeducacao.bol.uol.com.br/matematica/area-um-triangulo-pela-geometria-analitica.htm
|